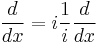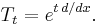Stone's theorem on one-parameter unitary groups
In mathematics, Stone's theorem on one-parameter unitary groups is a basic theorem of functional analysis which establishes a one-to-one correspondence between self-adjoint operators on a Hilbert space H and one-parameter families of unitary operators
which are strongly continuous, that is
and are homomorphisms:
Such one-parameter families are ordinarily referred to as strongly continuous one-parameter unitary groups. The theorem was proved by Marshall Stone (1930, 1932). Von Neumann (1932) showed that the condition that Ut is strongly continuous can be relaxed to say that it is weakly measurable, at least when the Hilbert space is separable.
Contents |
Formal statement
Let U be a strongly continuous 1-parameter unitary group, then there exists a unique self-adjoint operator A such that
Conversely, let A be a self-adjoint operator on a Hilbert space H. Then
is a strongly continuous one-parameter family of unitary operators.
The infinitesimal generator of {Ut}t is the operator 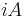 . This mapping is a bijective correspondence. A will be a bounded operator iff the operator-valued function
. This mapping is a bijective correspondence. A will be a bounded operator iff the operator-valued function 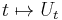 is norm continuous.
is norm continuous.
Stone's theorem can be recast using the language of Fourier transform. The real line R is a locally compact abelian group. Nondegenerate representations of the group C*-algebra C*(R) is in one-to-one correspondence with strongly continuous unitary representations R, i.e. strongly continuous one-parameter family of unitary operators. On the other hand, the Fourier transform is a *-isomorphism between C*(R) and C0(R), the C*-algebra of continuous functions on the line vanishing at infinity. So there is a one-to-one correspondence between strongly continuous one-parameter unitary groups and representations of C0(R). Since every representation of C0(R) corresponds to a self-adjoint operator, Stone's theorem holds.
The precise definition of C*(R) is as follows. Form the convolution algebra on Cc(R), the continuous functions of compact support, where the multiplication is convolution. The completion of this algebra in the L1 norm is a *-algebra, denoted by L1(R). C*(R) is then defined to be the enveloping C*-algebra of L1(R), i.e. its completion in the largest possible C*-norm. It is not trivial that C*(R) is isomorphic to C0(R), under the Fourier transform. A result in this direction is the Riemann–Lebesgue lemma, which says the Fourier transform maps L1(R) to C0(R).
Example
The family of translation operators
is a one-parameter unitary group of unitary operators; the infinitesimal generator of this family is an extension of the differential operator
defined on the space of complex-valued continuously differentiable functions of compact support on R. Thus
In other words, motion on the line is generated by the momentum operator.
Applications
Stone's theorem has numerous applications in quantum mechanics. For instance, given an isolated quantum mechanical system, with Hilbert space of states H, time evolution is a strongly continuous one-parameter unitary group on H. The infinitesimal generator of this group is the system Hamiltonian.
Generalizations
The Stone–von Neumann theorem generalizes Stone's theorem to a pair of self-adjoint operators, Q, P satisfying the canonical commutation relation, and shows that these are all unitarily equivalent to the position operator and momentum operator on L2(R).
The Hille–Yosida theorem generalizes Stone's theorem to strongly continuous one-parameter semigroups of contractions on Banach spaces.
References
- Neumann, J. von (1932), "Uber Einen Satz Von Herrn M. H. Stone" (in German), Annals of Mathematics, Second Series (Annals of Mathematics) 33 (3): 567–573, ISSN 0003-486X, http://www.jstor.org/stable/1968535
- Stone, M. H. (1930), "Linear Transformations in Hilbert Space. III. Operational Methods and Group Theory", Proceedings of the National Academy of Sciences of the United States of America (National Academy of Sciences) 16 (2): 172–175, ISSN 0027-8424, http://www.jstor.org/stable/85485
- Stone, M. H. (1932), "On one-parameter unitary groups in Hilbert Space", Annals of Mathematics 33 (3): 643–648, http://www.jstor.org/stable/1968538
- K. Yosida, Functional Analysis, Springer-Verlag, (1968)
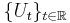
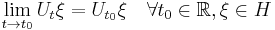
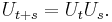
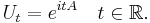
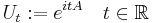
 = \psi(x %2B t) \quad](/2012-wikipedia_en_all_nopic_01_2012/I/e87e3e9e509ed8cdcf3911997fb91258.png)